
As you start looking at insulating materials like loft insulation you may quickly become bogged down by some quite complicated technical terms. In this article we look to simplify them, so you can hold your own when you are at the local DIY store!
Thermal Conductivity of insulating materials
Thermal conductivity, also known as Lambda (denoted by the greek symbol λ), is the measure of how easily heat flows through a specific type of material, independent of the thickness of the material in question.
The lower the thermal conductivity of a material, the better the thermal performance (i.e. the slower heat will move across a material).
It is measured in Watts per Metre Kelvin (W/mK).
To allow you to get a feel of insulating materials – their thermal conductivity varies between about 0.008 W/mK for vacuum insulated panels (so these are the best, but very expensive!) to about 0.061 W/mK for some types of wood fibre.
>>> CLICK TO LEARN MORE ABOUT U-VALUES OF INSULATING PRODUCTS <<<
If you were to use sheep’s wool to insulate you property this comes in about 0.034 W/mK, about the same as most of the other wool and fibre insulating materials.
R-Values
The R-value is a measure of resistance to heat flow through a given thickness of material. So the higher the R-value, the more thermal resistance the material has and therefore the better its insulating properties.
The R-value is calculated by using the formula
Where:
l is the thickness of the material in metres and
λ is the thermal conductivity in W/mK.
The R-value is measured in metres squared Kelvin per Watt (m2K/W)
For example the thermal resistance of 220mm of solid brick wall (with thermal conductivity λ=1.2W/mK) is 0.18 m2K/W.
If you were to insulate a solid brick wall, you simply find the R-value of the insulation and then add the two together. If you insulated this with 80mm thick foil-faced polyisocyanurate (with thermal conductivity λ=0.022W/mK and R-value of 0.08 / 0.022 = 3.64 m2K/W), you would have a total R-value for the insulated wall of 0.18 + 3.64 = 3.82 m2K/W. Therefore it would improve the thermal resistance by more than 21 times!

In real buildings a wall is made up of many different material layers. The total thermal resistance of the entire wall is calculated by adding the thermal resistance of each separate layer.
Unfortunately heat moves in and out of your home in several different ways and R-values only take into account conduction. It does not include either convection or radiation.
Therefore you may choose to use the U-value which takes into account all the different mechanisms of heat loss – read on to find out how this is calculated!
U-Values
The U value of a building element is the inverse of the total thermal resistance of that element. The U-value is a measure of how much heat is lost through a given thickness of a particular material, but includes the three major ways in which heat loss occurs – conduction, convection and radiation.
The environmental temperatures inside and outside a building play an important role when calculating the U-value of an element. If we imagine the inside surface of a 1 m² section of an external wall of a heated building in a cold climate, heat is flowing into this section by radiation from all parts of the inside the building and by convection from the air inside the building. So, additional thermal resistances should be taken into account associated with inside and outside surfaces of each element. These resistances are referred to as Rsi and Rso respectively with common values 0.12Km²/W and 0.06Km²/W for the internal and external surfaces, respectively.
This is the measure that is always within Building Regulations. The lower the U-value is, the better the material is as a heat insulator.
This is calculated by taking the reciprocal of the R-Value and then adding convection and radiation heat losses, as follows.
U = 1/ [ Rsi + R1 + R2 +… + Rso ]
In practise this is a complicated calculation, so it is best to use U-Value calculation software.
Units are in Watts per metre squared Kelvin (W/m2K).
As a guide an uninsulated cavity wall has a U-Value of approximately 1.6 W/m2K, while a solid wall has a U-Value of approximately 2 W/m2K
Using U-Values, R-Values and Thermal conductivity
If you are confronted with thermal conductivity, R-values and U-values going forward, here are 3 simple things to remember, to make sure you get the best insulating product.
- Higher numbers are good when comparing the Thermal Resistance and R-Values of products.
- Low numbers are good when comparing U-Values.
- The U-Value is the most accurate way to judge a material’s insulating ability, taking into account all the different ways in which heat loss occurs, however it is more difficult to calculate.
Installing energy saving technologies
Are you interested in installing home renewables? We have scoured the country for the best tradesmen, so that we can make sure we only recommend those we really trust. You can find one of these tradesmen on our easy to use local installer map.
>>> GO TO OUR LOCAL INSTALLER MAP NOW <<<
Alternatively, if you would like us to find you a local installer, just fill in the form below and we will be in touch shortly!
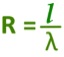














How can you have the thermal resistance of 220m of solid wall. Don’t you mean a wall of 225mm thick.
220m is bit longer than my road. Can’t imagine how to build a wall that thick.
the provided explanation is good and easy to understand Thanks.
220m of solid wall? I don’t understand
Solid wall is a wall without a cavity
I am confused; please help.
It is stated above that:-
R value = 1/λ
λ is the thermal conductivity in W/mK.
and
The R-value is measured in metres squared Kelvin per Watt (m2K/W)
I am confused as to where the extra m comes from: if you turn W/mK upside down, it looks as if you should get mK/W rather than m2K/W
Many thanks
R-value is “l” divided by λ, not 1 divided by λ, and as “l” is thickness in meter [m] units – you will get another [m] in units.
[R-value] = [m]/[W]/[m}[K] = [m2][K]/[W]
I was a little underwhelmed by the figures in the first example – that concluded that 80mm of PIR insulation would only double the insulation properties of a solid brick wall.
I think the measurement for the insulation was incorrectly specified as 8mm, (0.008m) – so should this calculation not read; (with an R-value of 0.08 / 0.022 = 3.63 m2K/W), Total = 3.63 + 0.29 = 3.92 m2K/W – thus improving the insulation of the 220mm brick wall by a factor of 13?
This sounds much more worthwhile… Or have I misunderstood?
When u convert 80mm to meter, answer is 008 m only. (80mm thick foil-faced polyisocyanurate)
90/1000=0.08
Where would you ever find a 220 meter thick brick wall? Confused?
It’s 220mm. Not mtr
220mm – thanks for spotting the typo!
I can’t understand the value of 220mm brick…
Plz tell me something about this..
220mm or 22cm is the length of a brick. The reason this is relevant is it is often the depth of a solid wall – where a brick is put at 90 degrees to the wall to tie two skins of brick together.
A modern brick measures 225 mm not 220mm, that missing 5 mm might make a difference in your calcs
What about the standard brick SIZE: 29 x 14 x 6.5 ?
how to calculate Equivalent U valve
very good best example on the net thank you for you time to put this on the net
I understand you explanation, but, our produces are 250mmx150mmx80mm, so yes we can calculate
the 80mm thickness but the end results is per square meter our product is 375 square cms would it be correct to pro rarta the heat transmission ?
A table of typical values would be appreciated including the effects of various treatments that will affect the u and r values.
I was also confused doing the R calculation. 1. The wall is 220 mm thick. 2. I also misread that R was the reciprocal of Lambda. It was not a 1, but L/R where L= thickness of the wall. 3.The “extra” M arrives when you use L (in metres) not a simple 1; so R = L (m)/(W/mK) = m2K/W. This is also for one square metre for one degree K temperture difference, so if you had a wall 150m2, you would have to multiply R by 150 and also the temperatue difference between inside and out. (I might be wrong, so please check!)
I had that same bloody problem mate
1/u= 1/u1+1/u2+1/u3+…….
is this formula correct
where u the total layer u value
un is the u value for each layer
1/(a+b) is not the same as 1/a + 1/b
I think this post is incorrect . I have seen the authoritative version as the same as the instructions on this site .
hi my name is big sam and I love science it smells so good !
Confused the hell out of me. In your example “For example the thermal resistance of 220mm of solid brick wall (with thermal conductivity λ=1.2W/mK) is 0.18 m2K/W.”, how did you find the 0.18???
Its the thickness in meters not millimeters. So it’s 0.22/1.2 =0.18
I have to write down what an interaction between the 3 values is, or more interactions if possible. Can somebody help me?
As a guide an uninsulated cavity wall has a U-Value of approximately 1.6 W/m2K, while a solid wall has a U-Value of approximately 2 W/m2K
The 1.6 looks like 16.
in U value… the unit is m2.. i want to know which 2 dimensions should be multiplied to get square of metre…
I’ll admit straight off that I didn’t try to do the math on this, definitely not my forte. I was simply trying to get a feel for how much more efficient a .25 U window is compare to a .28 U. I’ve been told that anything below .3 U is an efficient window but does it make sense to keep pushing downward. On my current project the .25 U window package comes out to roughly $3K more. Is it possible to calculate the time to pay off additional cost? I’m guessing (emphasize guessing) that it would take over 50 years.
Be aware that there are metric and imperial U and R values, which is why you (imperial) are getting 0.3 whereas me I’m getting 0.7
The biggest difference I’ve seen is warmth of the room. If you have large amounts of glass and the rest is well insulated – the window areas become a cold zone. You also need to realise that the people in the room generate heat! What you can do is get close to a passive house, in that the heating isn’t on but the house stays warm.
As to payback timescales, that has to be done on a house-by-house basis. There are a large number of factors (inc. outside temp/inside temp/occupancy profile/occupancy load/other insulation) that determine payback. My personal opinion is how long do intend to keep the property? As you don’t want to replace the windows every 5 years.
What’s the best way to improve the U-Value of a solid walled house from the inside? It’s original brickwork and we don’t want to cover it up so solid was insulation is not an option.
Hi Mark,
There are internal options, but have you considered recreating the brickwork with brick slips? Take a look at this article, it might change your mind about the EWI possibilities…
Thanks,
Harriet
Thank you for simplifying this! seems so much less complicated now.
Can someone point out the real U value formula where solar insulation on wall material is taken into account. This formula (pointed out in article) is useful only in labs where there is no sun radiation which heats up the wall even in cloudy winter days. The insolation value was taken out somewhere in 80’s when there was necessity to sell rock/glass wool to non educated consumers. The reason was if you take the sun into equation there is almost no commercial sense to isolate the wall from the sun with low thermal mass materials such as wool. This means everybody is chasing around U values which are made up by wool manufacturers not physics. That would not be a problem if only the vapor barrier and incapability to withstand water (minerals wool) results in molds that ruin wooden structures and health (cancer, lung diseases) of inhabitants.