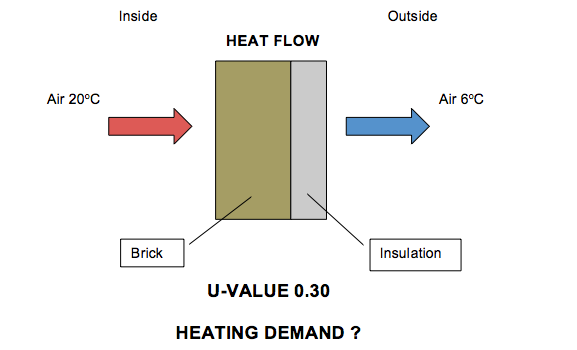
In this article we are going to figure out the effect of U-values on the heating demand of your home. By adding insulation to the walls of your home, you reduce the U-value and in turn you will save money on your heating energy bills. Let see how this works.
The heat demand of your house depends on a number of factors such as:
- The insulating properties of the fabric of your house, known as U-values of the walls
- The amount of heat carried out of your house by air movement, depending on how big your house is and the number of windows
- The difference between the inside and outside temperatures – the heat requirement for a home varies from season to season (more heat is needed during the winter months for example).
A better way to estimate the annual space heat consumption is to divide the heating into periods for different outside temperatures, such as mid-season and winter. For example, during winter the average outside temperature is 6oC while the inside temperature is set to 20oC to stay comfortable. For a standard temperature difference and constant heat losses through ventilation, the amount of heating required depends on the insulation of the walls, roof and floor. In the next section we are going to examine how insulation affects the heat transfer through the walls.
How does U value change when cavity or solid walls are insulated?
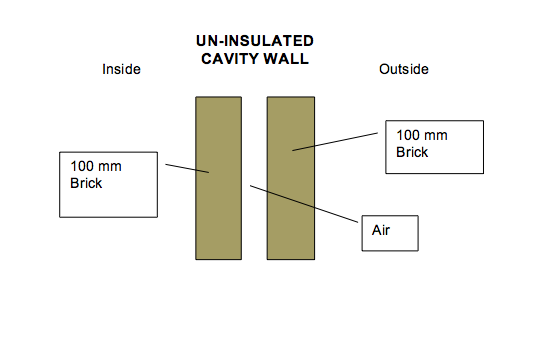
Common cavity walls built after 1930s consist of two layers of brick of about 100mm each separated by an air cavity of 70mm in the middle as you see in the picture below.
The u-value of an Un-insulated Wall
| Layers | Thickness (m) | Conductivity (W/mK) | Resistance (Km²/W) |
| Internal surface | – | – | 0.12 |
| 100 mm Brick | 0.100 | 1.2 | 0.08 |
| Air | 0.070 | – | 0.17 |
| 100 mm Brick | 0.100 | 1.2 | 0.08 |
| External surface | – | – | 0.06 |
| Sum | 0.270 | – | 0.52 |
| U value (W/m²K) | 1.94 | ||
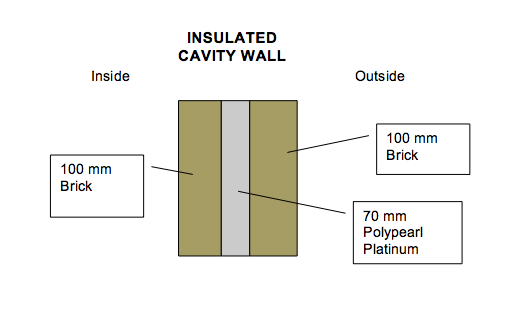
The insulation commonly used in cavity walls like this is EPS (such as Polypearl Plus and Polypearl Platinum) – this is expanded polystyrene bead which helps to reduce the thermal transmittance of the external cavity walls. By adding 70mm of Polypearl Platinum insulation to your cavity wall you can reduce the U-value from 1.94W/m²K to 0.41W/m²K.
The u-value of a cavity wall insulated with Polypearl Platinum (EPS Insulation)
| Layers | Thickness (m) | Conductivity (W/mK) | Resistance (Km²/W) |
| Internal surface | – | – | 0.12 |
| 100 mm Brick | 0.100 | 1.2 | 0.08 |
| 70mm Polypearl Platinum | 0.070 | 0.033 | 2.12 |
| 100 mm Brick | 0.100 | 1.2 | 0.08 |
| External surface | – | – | 0.06 |
| Sum | 0.270 | – | 2.47 |
| U value (W/m²K) |
0.41 |
||
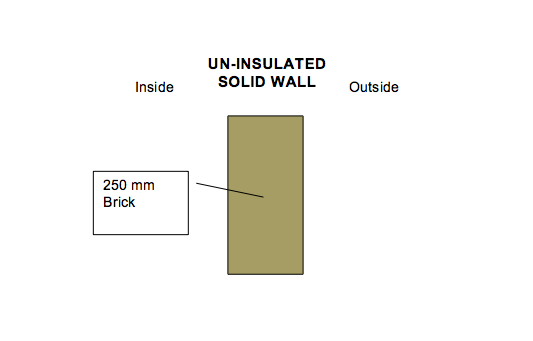
The u-value of an Uninsulated Solid Wall
Solid Walls commonly consist of a brick layer of 250mm thick. Most houses built before the 1930s (and many blocks of flats up to the 1950s) have solid walls without any insulation – these tend to suffer from large heat losses with U-values reaching as high as 2.58W/m²K.
| Layers | Thickness (m) | Conductivity (W/mK) | Resistance (Km²/W) |
| Internal surface | – | – | 0.12 |
| 250 mm Brick | 0.250 | 1.2 | 0.21 |
| External surface | – | – | 0.06 |
| Sum | 0.250 | – | 0.39 |
|
U value (W/m²K) |
2.58 | ||
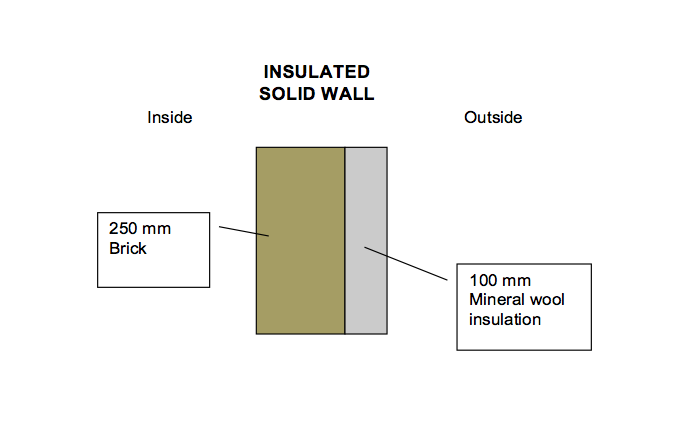
Insulated Solid Wall
By adding 100mm of mineral wool or expanded polystyrene (EPS) in your solid walls you can reach a U-value of 0.31W/m²K and 0.28W/m²K, respectively.
Mineral wool insulation
| Layers | Thickness (m) | Conductivity (W/mK) | Resistance (Km²/W) |
| Internal surface | – | – | 0.12 |
| 250 mm Brick | 0.250 | 1.2 | 0.21 |
| 100mm Mineral wool | 0.100 | 0.035 | 2.86 |
| External surface | – | – | 0.06 |
| Sum | 0.350 | – | 3.25 |
|
U value (W/m²K) |
0.31 | ||
EPS
| Layers | Thickness (m) | Conductivity (W/mK) | Resistance (Km²/W) |
| Internal surface | – | – | 0.12 |
| 250 mm Brick | 0.250 | 1.2 | 0.21 |
| 100mm EPS | 0.100 | 0.032 | 3.13 |
| External surface | – | – | 0.06 |
| Sum | 0.350 | – | 3.51 |
|
U value (W/m²K) |
0.28 | ||
What is the impact on U-value of adding even more insulation to walls?
In the table we have figured out the reduction of the U-values by adding different thicknesses and types of insulation in a solid brick wall and a cavity wall. As you can see there is no need to go for insulation thickness higher than 100mm as you can reach the U-values required to meet building regulations.
| COMMON BRICK (250mm) | ||
| Insulation Thickness (mm) | U-value (W/m2K) | |
| UNINSULATED WALL | – | 2.58 |
| EPS | 50 | 0.51 |
| 100 | 0.28 | |
| 150 | 0.20 | |
| Mineral wool | 50 | 0.55 |
| 100 | 0.31 | |
| 150 | 0.21 | |
| CAVITY WALL | ||
| Insulation Thickness (mm) | U-value (W/m2K) | |
| UNINSULATED WALL | – | 1.94 |
| Polypearl Platinum | 50 | 0.54 |
| 70 | 0.41 | |
| 150 | 0.20 | |
| Polypearl Plus | 50 | 0.59 |
| 70 | 0.45 | |
| 150 | 0.23 | |
What practically a reduction of the U-value means?
This is an example to help you understand how U-values affect the heat losses of your walls.
The heat loss through the walls can be described by the equation:
Fabric Heat loss through the walls = Σ UxA x ΔΤ, where
Σ UxA is the sum of the products of the U values and areas of all parts of the external envelope of the building,
ΔΤ is the difference between external and internal temperatures
So, for 1m2 of solid un-insulated wall and 20oC – 6oC = 14oC = 14K the heat loss would be 2.58 W/m2K x 14 K = 36.12W/m2 as can be seen in the next table.
| U value (W/m2K) | ΔΤ (K) | Heat Demand (W/m2) | Reduction of heat losses (W/m2) | |
| Un-insulated wall | 2.58 | 14 | 36.12 | – |
| Mineral wool insulation | 0.31 | 14 | 4.34 | 31.78 |
| EPS insulation | 0.30 | 14 | 3.92 | 32.20 |
By adding insulation e.g.. mineral wool there would be a reduction of 2.58 – 0.31 = 2.27 W/m2K in the U-value of the solid wall. Smaller U-values practically means a reduction in heat loss of 31.78W/m2.
We should also take into account the air leakage of your house to estimate the heat demand of your house. For example, for an average semi-detached house of 98 m2 with a total volume of 245 m3 the heat loss coefficient is cf = 304.02 W/K for un-insulated walls and standard U-values for the windows, floor and roof as you see in the next table. For the same house, the ventilation loss coefficient cv = 65 W/K. By insulating the wall with mineral wool the fabric heat losses will be reduced to cf = 202.03 W/K.
| U-value (W/m²K) | A.U (W/K) | ||||
| Element | Area (m2) | Un-insulated wall | Mineral wool | Un-insulated wall | Mineral wool |
| Wall | 89 | 2.58 | 0.31 | 229.62 | 27.59 |
| Windows (8m2 south, 8m2 north) | 16 | 2.50 | 2.50 | 40.0 | 40.00 |
| Floor | 49 | 0.45 | 0.45 | 22.1 | 22.1 |
| Roof | 49 | 0.25 | 0.25 | 12.3 | 12.3 |
| TOTAL | 203 | 304.02 | 101.99 | ||
| Difference | 202.03 | ||||
So, the new heat demand would be:
Heat demand/ m2 = (202.03W/K + 65 W/K) / 14K = 19.07W/m2
If you heat your house with gas (4.36p per KWh), this practically means that you will have saved about 0.01907KWh/m2 x £0.0436/KWh = £0.00083145/m2 per hour. During the heating season, if you heat your house for 7 hours you will save about £0.0058/m2 per day. So, for the whole heating period of approximately 3 months you will save £0.524/m2. For an average house of 98m2 this means that you save £51.35 to heat your house by adding mineral wool insulation to your solid walls.
| U value (W/m2K) | ΔΤ (K) | Reduction of heat losses (W/m2) | Save (£) | |
| Mineral wool insulation | 0.31 | 14 | 31.78 | 51.35 |
| EPS insulation | 0.30 | 14 | 32.20 | 52.90 |
In reality, in order to give a more accurate estimation of the heat demand we should take into account the heat gains from the lights and electrical appliances of your home, and the heat produced by the occupants and the solar heat gains mainly through windows. So, actually the heating loads will be a little bit less than calculated in this example – the difference between the heat losses and the heat gains.











Useful post, thanks.
Hi
Probably the best post for a layman I’ve come across on the matter, but could still be improved by explaining the rationale for why ventilation coefficient falls to just 65 a bit better and also a comparison table for a small, average and larger homes.